Implementing Navigation Meshes

In my previous blog post, I explained what navigation meshes are and why they’re essential for my game. In this post, I’ll walk you through how I implemented this functionality in my game engine, breaking down the process step by step.

Step 1: Creating Native Polygons

The foundation of the navigation mesh is a set of “native” polygons that define all walkable areas in the game. I call them “native” because the mesh generation process relies on them. To create these polygons, I added tools to draw, edit, and save them within the engine. For now, this manual approach works well since the map is relatively small, but I’m considering automating this process in the future to handle larger or more complex maps.

Here’s an example of the native polygons:

In the image, you can see five polygons. It’s critical that these polygons share edges to ensure proper adjacency. You might notice some polygons have degenerate vertices—vertices that could be omitted—but these are necessary to maintain shared edges between polygons. To address this inconvenience, I plan to implement a check to detect if a polygon’s edges are parallel and intersect, which should help clean up these cases.

Step 2: Partitioning into Convex Polygons

As discussed in my previous post, navigation meshes require convex polygons for efficient pathfinding. To achieve this, I used a tiny polygon partitioning library and integrated a few of its functions into my engine. Specifically, I utilized the library’s convex partitioning function, which first triangulates a polygon using the Ear Clipping algorithm and then merges triangles where possible to create larger, convex shapes.

Here’s how the partitioned mesh looks: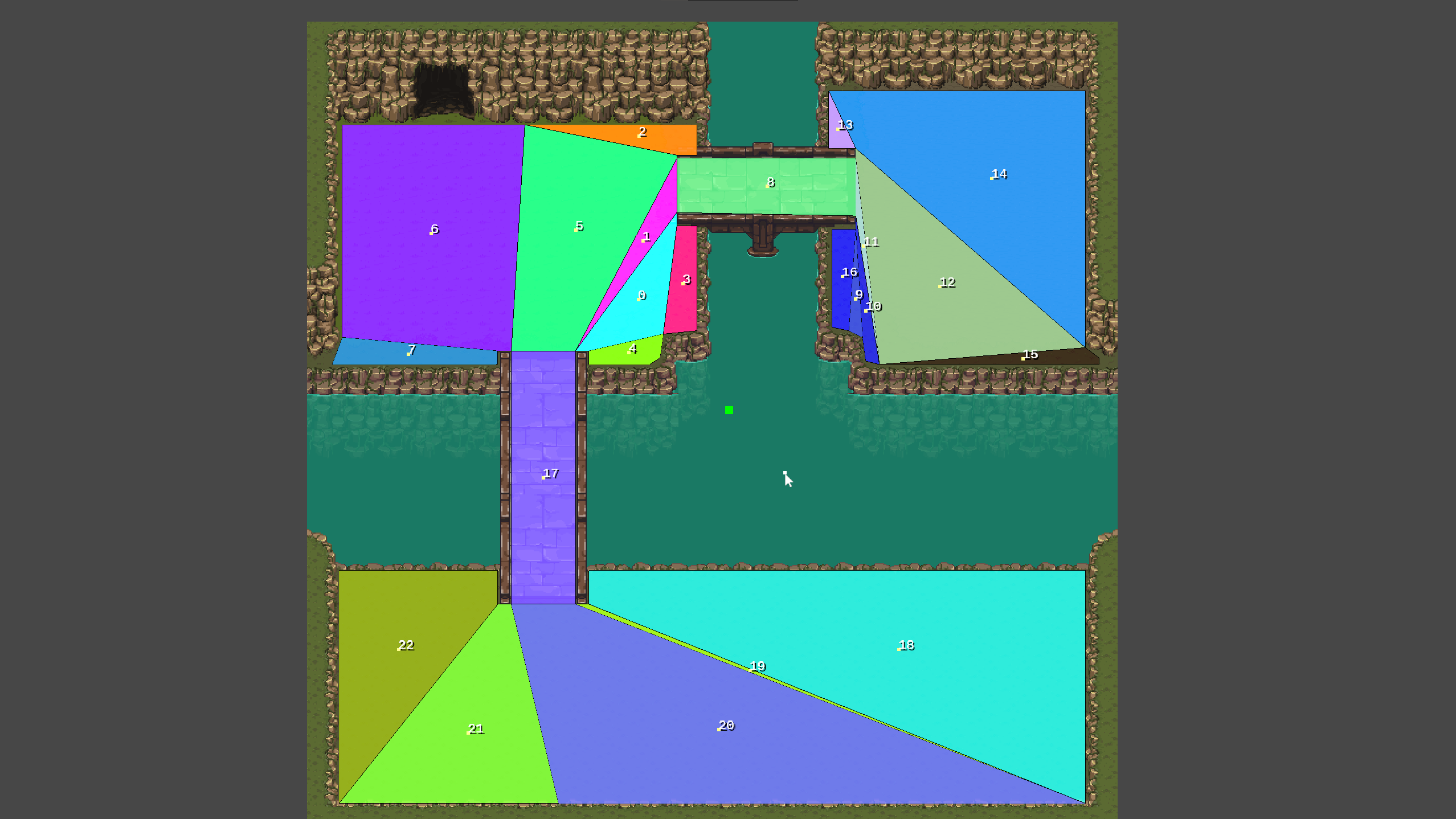

As shown, all resulting shapes are convex, which is great. However, some polygons are narrow triangles, which aren’t ideal for navigation meshes as they can complicate pathfinding. For now, I’ve decided to leave them as is, but if they cause issues, I may either split the native polygons into smaller pieces or add extra points during partitioning to improve the results.

Next, I iterate through the convex polygons to create an array of navigation nodes for the A* algorithm. For each polygon, I calculate its center point and bounding box, which simplifies the process of identifying the correct polygon during pathfinding.

After generating the nodes, I iterate again to determine adjacencies. Two polygons are considered adjacent if they share an edge. When an adjacency is found, I increment a neighbor count and store a pointer to the neighboring node. During this process, I also create a hash table to store edge data, which is crucial for maintaining consistent vertex ordering.

The hash table uses an edge as the key and stores data in the following format:

 {PolyA_ID, Edge_A_Vertex, Edge_B_Vertex}
 {PolyB_ID, Edge_A_Vertex, Edge_B_Vertex}

Here’s an illustration of how the mesh polygons are connected:

Step 4: Ensuring Consistent Vertex Ordering

After partitioning, all polygons are oriented counterclockwise, meaning their vertices are ordered from left to right. This consistency is vital for the Funnel Algorithm (described later) to work correctly. The hash table ensures that vertex ordering remains consistent when moving between polygons.

For example, consider two polygons, P1 and P2, that share an edge defined by vertices A and B. For P1, the left vertex of the edge is A, and the right is B. For P2, it’s the opposite: the left vertex is B, and the right is A. When moving from P1 to P2, the vertex order is correct, but when moving from P2 to P1, the vertices must be reordered to maintain consistency.

Here’s an illustration of this concept:

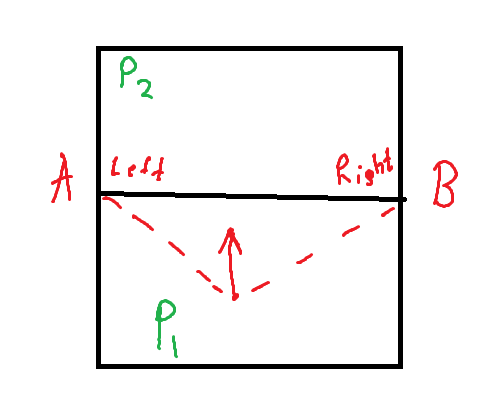
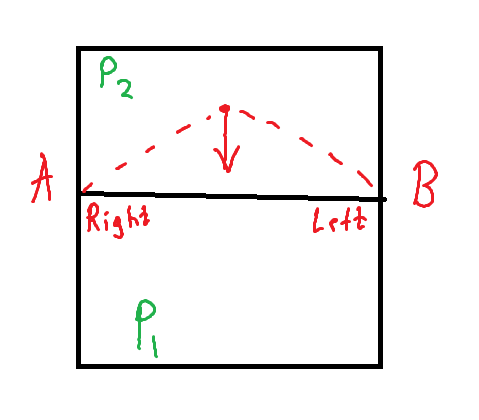
On the left image we move from P1 to P2 and on the right image from P2 to P1

Step 5: Pathfinding with A* and the Funnel Algorithm

With the navigation mesh set up, we can now find a path between a start and end position. For this example, the green square represents the start position, and the red square represents the end position.

Finding the Start and End Polygons

First, I identify which polygons contain the start and end points. I iterate through the mesh nodes, checking if each point lies within a polygon’s bounding box. If it does, I perform a point-in-polygon test to confirm. For this example, the start point is in polygon 21, and the end point is in polygon 18.

Running A* Pathfinding

Using the A* algorithm, I find the shortest path between the start and end polygons in terms of polygon traversals. The red line in the image below shows the sequence of polygons to follow: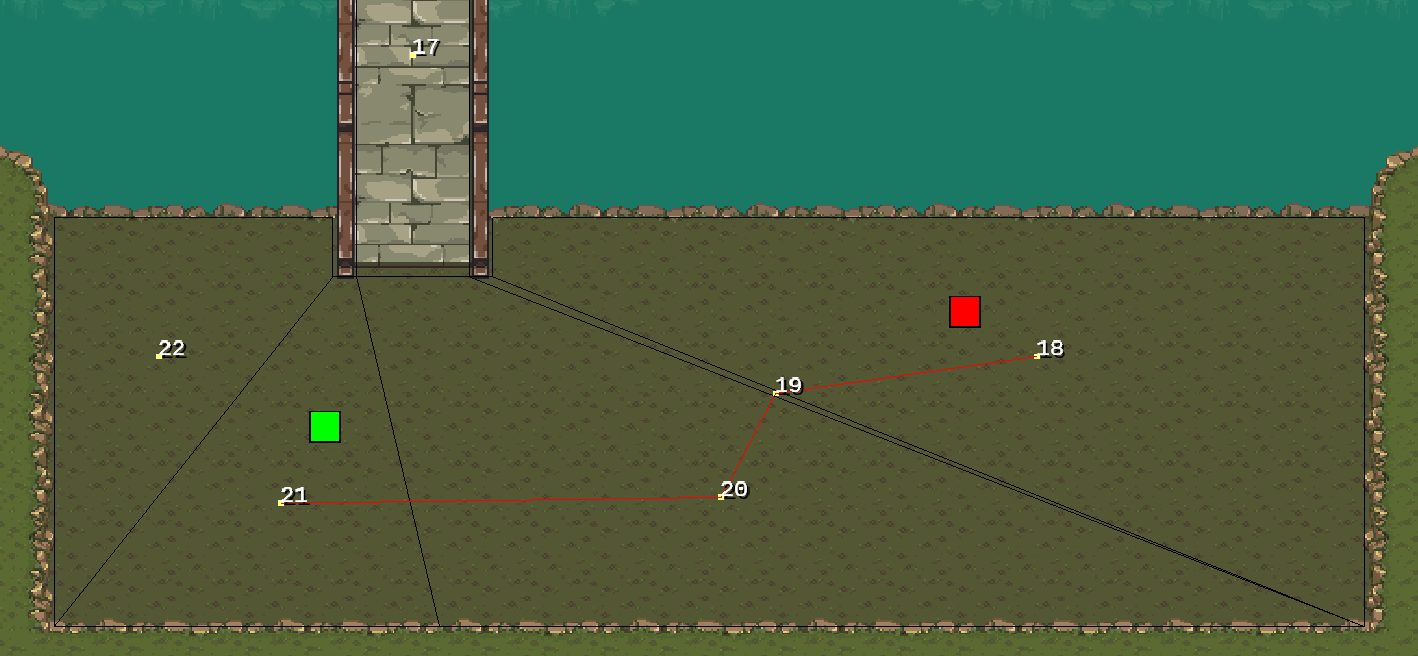

Building the Portal Array

After solving A*, I create a portal array for the Funnel Algorithm. The first portal is the start position. Then, for each edge in the A* path, I look up the hash table to determine the correct vertex order and add the vertices to the portal array. The final portal is the end position.

Here’s how the portals (edges) look, with blue squares indicating the left vertex of each portal: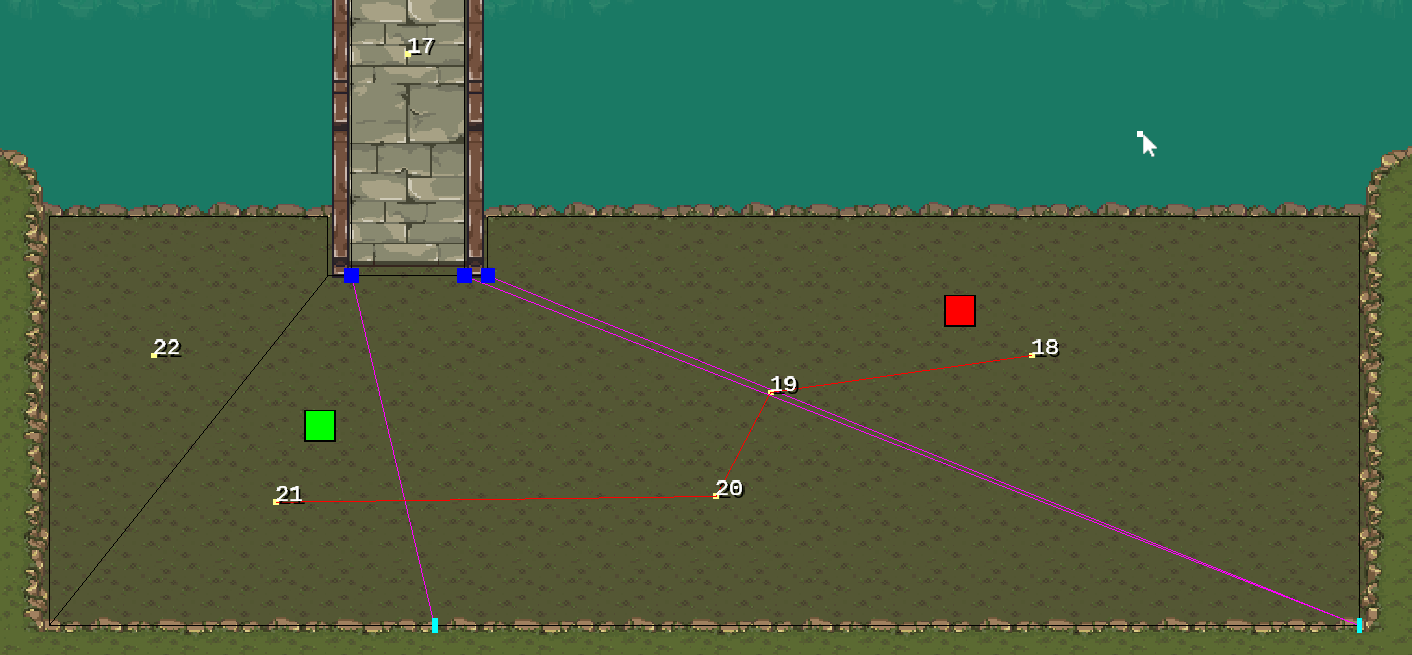

If we swap the start and end positions, the portal ordering adjusts accordingly:

Portals (Still moving from Green to Red)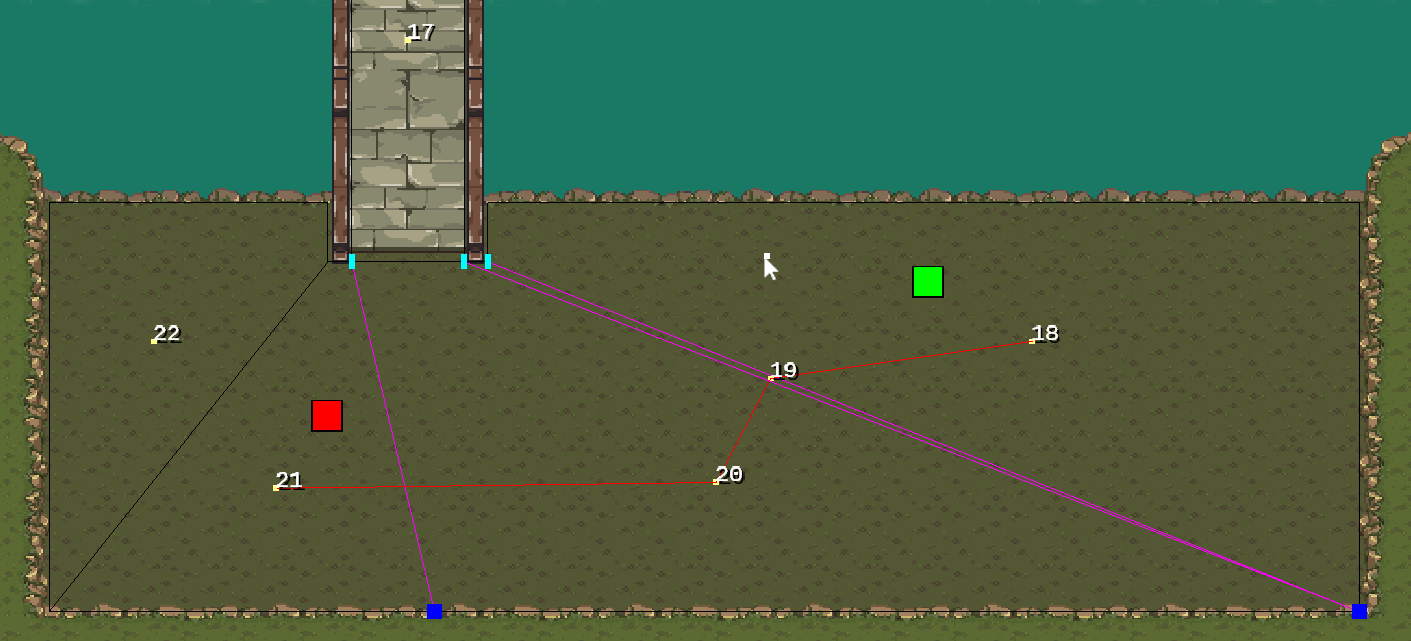

Applying the Funnel Algorithm

Finally, I use the Funnel Algorithm (also known as String Pulling) in its simplest form to compute the straightest possible path through the portals. This produces an optimal path from the start to the end position.

Here’s an illustration of how String Pulling works: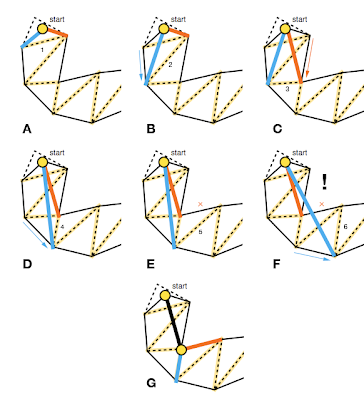

The resulting path is shown below:

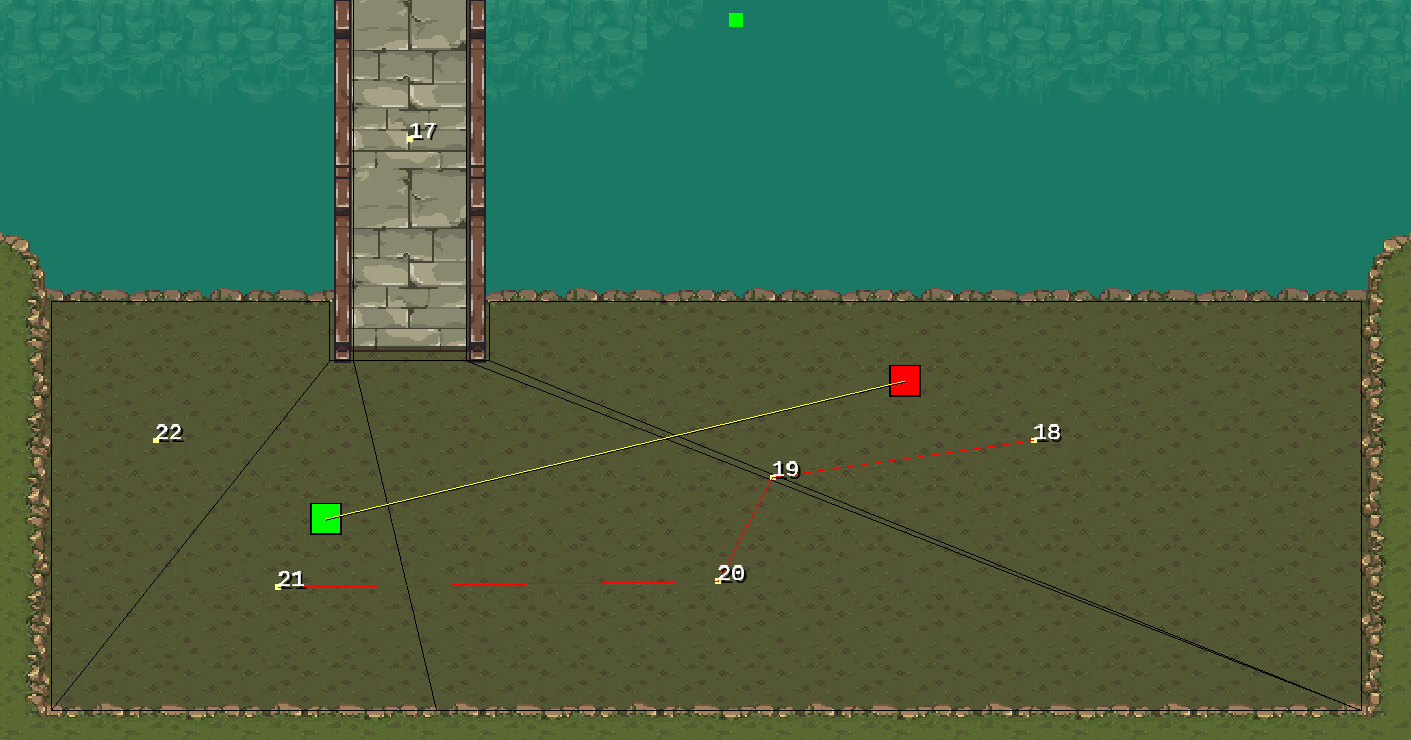
For comparison, if this were a grid-based system, the path might look like this:

Grid-Based Path with smoothing from the game simulation

Conclusion

This implementation creates an efficient navigation mesh that allows characters to move smoothly from one point to another. While there are areas for improvement, such as handling narrow triangles or automating native polygon creation, the current system works well for my game’s needs.

Here are the resources I used:

And here’s a code snippet from my implementation (sorry in advance for not convinient view):

Show Code

struct neighbour_edge
{
    world_position A;
    world_position B;
};

struct world_polygon_list
{
    world_polygon Poly;
    polygon2 RealPoly;

    world_polygon_list *Next;
    world_polygon_list *Prev;
};

struct nav_poly_node
{
    world_position TileP;

    s32 Index;
    world_polygon_list *PolyPtr;
    
    b32 Visited;

    r32 GlobalGoal;
    r32 LocalGoal;

    rectangle2i Bounds;

    s32 NeighbourCount;
    nav_poly_node *Neighbours[8];
    neighbour_edge NEdge[8];
    
    nav_poly_node *Parent;
};

inline r32
DistanceBetween(world *World, nav_poly_node *NodeA, nav_poly_node *NodeB)
{
    v2 Delta = Subtract(World, &NodeA->TileP, &NodeB->TileP);

    r32 Result = SquareRoot(Square(Delta.x) + Square(Delta.y));

    return(Result);
}

internal nav_poly_node *
SolvePolyAStar(editor_mode_game *GameMode, nav_poly_node *Start, nav_poly_node *End)
{
    TIMED_FUNCTION();

    if(Start && End)
    {
        for(u32 NodeIndex = 0;
            NodeIndex < GameMode->PolyNodeCount;
            ++NodeIndex)
        {
            nav_poly_node *Node = GameMode->PolyNodes + NodeIndex;
            Node->Visited = false;
            Node->GlobalGoal = Real32Maximum;
            Node->LocalGoal = Real32Maximum;
            Node->Parent = 0;
        }

        nav_poly_node *CurrentNode = Start;
        CurrentNode->LocalGoal = 0.0f;
        CurrentNode->GlobalGoal = DistanceBetween(GameMode->WorldState->World, Start, End);

        heap *Heap = &GameMode->MinPolyNodeHeap;

        sort_entry Key = {};
        Key.Index = Start->Index;
        Key.SortKey = Start->GlobalGoal;
        MinHeapInsertNode(Heap, Key);

        while((Heap->Size != 0) && (CurrentNode != End))
        {
            nav_poly_node *TestNode = GameMode->PolyNodes + Heap->Nodes[0].Index;
            while((TestNode->Visited) && (Heap->Size != 0))
            {
                MinHeapExtractNode(Heap);
                TestNode = GameMode->PolyNodes + Heap->Nodes[0].Index;
            }

            if(Heap->Size == 0)
            {
                break;
            }

            CurrentNode = GameMode->PolyNodes + Heap->Nodes[0].Index; 
            CurrentNode->Visited = true;

            for(s32 NeighbourIndex = 0;
                NeighbourIndex < CurrentNode->NeighbourCount;
                ++NeighbourIndex)
            {
                nav_poly_node *NeighbourNode = CurrentNode->Neighbours[NeighbourIndex];
                if(NeighbourNode)
                {
                    if((!NeighbourNode->Visited))
                    {
                        sort_entry Key = {};
                        Key.Index = NeighbourNode->Index;
                        Key.SortKey = NeighbourNode->GlobalGoal;

                        r32 LowerGoal = CurrentNode->LocalGoal + DistanceBetween(GameMode->WorldState->World, CurrentNode, NeighbourNode);
                        if(LowerGoal < NeighbourNode->LocalGoal)
                        {
                            NeighbourNode->Parent = CurrentNode;
                            NeighbourNode->LocalGoal = LowerGoal;

                            NeighbourNode->GlobalGoal = (NeighbourNode->LocalGoal +
                                                         DistanceBetween(GameMode->WorldState->World, NeighbourNode, End));
                            Key.SortKey = NeighbourNode->GlobalGoal;
                        }

                        MinHeapInsertNode(Heap, Key);
                    }
                }
            }
        }

        ZeroArray(Heap->MaxSize, Heap->Nodes);
        Heap->Size = 0;
    }

    return(End);
}

internal s32
StringPull(v2 *Portals, s32 PortalsCount, v2 *Points, s32 MaxPoints)
{
    TIMED_FUNCTION();

    f32 Epsilon = 0.001f;
    // Find straight path.
    s32 PointsCount = 0;

    // Init scan state
    s32 ApexIndex = 0;
    v2 PortalApex = Portals[0];

    s32 LeftIndex = 0;
    v2 PortalLeft = Portals[0];

    s32 RightIndex = 0;
    v2 PortalRight = Portals[1];

    // Add start point.
    Points[0] = PortalApex;
    PointsCount++;

    for(int i = 1; i < PortalsCount && PointsCount < MaxPoints; ++i)
    {
        v2 left = Portals[i*2];
        v2 right = Portals[i*2 + 1];

        // Update right vertex.
        if(TriangleArea2(PortalApex, PortalRight, right) <= 0.0f)
        {
            if(PointsAreEqual(PortalApex, PortalRight, Epsilon) ||
               TriangleArea2(PortalApex, PortalLeft, right) > 0.0f)
            {
                // Tighten the funnel.
                PortalRight = right;
                RightIndex = i;
            }
            else
            {
                // Right over left, insert left to path and restart scan from portal left point.
                Points[PointsCount++] = PortalLeft;

                // Make current left the new apex.
                PortalApex = PortalLeft;
                ApexIndex = LeftIndex;
                // Reset portal
                PortalLeft = PortalApex;
                PortalRight = PortalApex;

                LeftIndex = ApexIndex;
                RightIndex = ApexIndex;

                // Restart scan
                i = ApexIndex;
                continue;
            }
        }

        // Update left vertex.
        if(TriangleArea2(PortalApex, PortalLeft, left) >= 0.0f)
        {
            if(PointsAreEqual(PortalApex, PortalLeft, Epsilon) ||
               TriangleArea2(PortalApex, PortalRight, left) < 0.0f)
            {
                // Tighten the funnel.
                PortalLeft = left;
                LeftIndex = i;
            }
            else
            {
                // Left over right, insert right to path and restart scan from portal right point.
                Points[PointsCount++] = PortalRight;

                // Make current right the new apex.
                PortalApex = PortalRight;
                ApexIndex = RightIndex;
                // Reset portal
                PortalLeft = PortalApex;
                PortalRight = PortalApex;

                LeftIndex = ApexIndex;
                RightIndex = ApexIndex;

                // Restart scan
                i = ApexIndex;
                continue;
            }
        }
    }

    // Append last point to path.
    if(PointsCount < MaxPoints)
        Points[PointsCount++] = Portals[(PortalsCount - 1)*2];

    return(PointsCount);
}

internal void
PartitionNavigationMesh(editor_mode_game *GameMode, sim_region *SimRegion, memory_arena *TempArena)
{
    // NOTE(paul): Clear Mesh Polygon List
    for(world_polygon_list *Iter = GameMode->MeshPolygonsSentinal.Next;
        Iter != &GameMode->MeshPolygonsSentinal;
        )
    {
        world_polygon_list *T = Iter;
        Iter = T->Next;

        DLIST_REMOVE(T);
        Platform.DeallocateMemory(T->Poly.Vertices);
        Platform.DeallocateMemory(T);
    }
                            
    PartitionPolies(GameMode, SimRegion, TempArena);

    // NOTE(paul): Clear node neighbours count
    for(u32 I = 0;
        I < GameMode->PolyNodeCount;
        ++I)
    {
        nav_poly_node *Node = GameMode->PolyNodes + I;
        Node->NeighbourCount = 0;
    }

    for(u32 I = 0;
        I < GameMode->EdgeTable.Size;
        ++I)
    {
        hash_table_entry *Scan = GameMode->EdgeTable.Hash[I];
        while(Scan)
        {
            hash_table_entry *Entry = Scan;
            Scan = Scan->Next;

            Entry->Next = GameMode->EdgeTable.Free;
            GameMode->EdgeTable.Free = Entry;
        }
    }
    
    GameMode->PolyNodeCount = 0;                            

    polygon2 RealPoly = {};
    RealPoly.Vertices = PushArray(TempArena, 128, v2);

    s32 PIndex = 0;
    for(world_polygon_list *Iter = GameMode->MeshPolygonsSentinal.Next;
        Iter != &GameMode->MeshPolygonsSentinal;
        Iter = Iter->Next)
    {
        world_polygon *Poly = &Iter->Poly;
        ConvertWorldPolygonToPolygon2(GameMode->WorldState->World, &SimRegion->Origin, Poly, &RealPoly);
        Iter->RealPoly = RealPoly;

        v2 Center = {};
        f32 SignedArea = 0.0f;
        for(s32 I = 0; I < RealPoly.VertexCount; ++I)
        {
            v2 p0 = RealPoly.Vertices[I];
            v2 p1 = RealPoly.Vertices[(I + 1) % RealPoly.VertexCount];

            f32 C = Cross(p0, p1);
            SignedArea += C;

            Center += (p0 + p1)*C;
        }

        SignedArea *= 0.5f;
        if(AbsoluteValue(SignedArea) > 0)
            Center *= 1.0f / (6.0f*SignedArea);

        rectangle2i Bounds = CalculatePolygonBoundingBox(Poly);

        nav_poly_node *Node = GameMode->PolyNodes + GameMode->PolyNodeCount++;                                
        InitNavPolyNode(Node, (GameMode->PolyNodeCount - 1), Iter,
                        MapIntoTileSpace(GameMode->WorldState->World, SimRegion->Origin, Center),
                        Bounds);
        PIndex += 1;
    }

    // NOTE(paul): Build conectivity graph
    s32 I1 = 0;
    for(world_polygon_list *Iter = GameMode->MeshPolygonsSentinal.Next;
        Iter != &GameMode->MeshPolygonsSentinal;
        Iter = Iter->Next)
    {
        world_polygon *Poly = &Iter->Poly;
        
        s32 Orientation = GetPolygonOrientation(&Iter->RealPoly); 
        Assert(Orientation == POLY_ORIENTATION_CCW)
                                
        s32 I2 = I1 + 1;
        for(world_polygon_list *Iter2 = Iter->Next;
            Iter2 != &GameMode->MeshPolygonsSentinal;
            Iter2 = Iter2->Next)
        {
            world_polygon *Poly2 = &Iter2->Poly;

            s32 Orientation2 = GetPolygonOrientation(&Iter2->RealPoly); 
            Assert(Orientation2 == POLY_ORIENTATION_CCW)

            b32 Found = false;
            for(s32 I = 0; I < Poly->VertexCount; ++I)
            {
                world_position A1 = Poly->Vertices[I];
                world_position B1 = Poly->Vertices[(I + 1) % Poly->VertexCount];
                hash_key HashKey = {};
                HashKey.WorldEdge.A = A1;
                HashKey.WorldEdge.B = B1;
                
                for(s32 J = 0; J < Poly2->VertexCount; ++J)
                {
                    world_position A2 = Poly2->Vertices[J];
                    world_position B2 = Poly2->Vertices[(J + 1) % Poly2->VertexCount];

                    if(((A1.TileX == B2.TileX) && (A1.TileY == B2.TileY)) &&
                       ((B1.TileX == A2.TileX) && (B1.TileY == A2.TileY)) &&
                       ((A1.Offset.x == B2.Offset.x) && (A1.Offset.y == B2.Offset.y)) &&
                       ((B1.Offset.x == A2.Offset.x) && (B1.Offset.y == A2.Offset.y)))
                    {
                        hash_data Data = {};
                        Data.PolyMeshAdjacency = {(u32)I1, A1, B1, (u32)I2, A2, B2};
                        InsertKey(&GameMode->EdgeTable, HashKey, Data, &GameMode->NavMeshArena);

                        nav_poly_node *Poly1Node = GameMode->PolyNodes + I1;
                        nav_poly_node *Poly2Node = GameMode->PolyNodes + I2;
                        if(Poly1Node->NeighbourCount == 0)
                        {
                            Poly1Node->Neighbours[Poly1Node->NeighbourCount] = Poly2Node;
                            Poly1Node->NEdge[Poly1Node->NeighbourCount] = {A1, B1};
                            ++Poly1Node->NeighbourCount;
                        }
                        else
                        {
                            b32 IsNew = true;
                            for(s32 NI = 0;
                                NI < Poly1Node->NeighbourCount;
                                ++NI)
                            {
                                nav_poly_node *Test = Poly1Node->Neighbours[NI];
                                if(Test->Index == I2)
                                {
                                    IsNew = false;
                                    break;
                                }
                            }

                            if(IsNew)
                            {
                                Poly1Node->Neighbours[Poly1Node->NeighbourCount] = Poly2Node;
                                Poly1Node->NEdge[Poly1Node->NeighbourCount] = {A1, B1};
                                ++Poly1Node->NeighbourCount;
                            }
                        }

                        if(Poly2Node->NeighbourCount == 0)
                        {
                            Poly2Node->Neighbours[Poly2Node->NeighbourCount] = Poly1Node;
                            Poly2Node->NEdge[Poly2Node->NeighbourCount] = {A1, B1};
                            ++Poly2Node->NeighbourCount;
                        }
                        else
                        {
                            b32 IsNew = true;
                            for(s32 NI = 0;
                                NI < Poly2Node->NeighbourCount;
                                ++NI)
                            {
                                nav_poly_node *Test = Poly2Node->Neighbours[NI];
                                if(Test->Index == I1)
                                {
                                    IsNew = false;
                                    break;
                                }
                            }

                            if(IsNew)
                            {
                                Poly2Node->Neighbours[Poly2Node->NeighbourCount] = Poly1Node;
                                Poly2Node->NEdge[Poly2Node->NeighbourCount] = {A1, B1};
                                ++Poly2Node->NeighbourCount;
                            }
                        }

                        Found = true;
                        break;
                    }
                }

                if(Found)
                    break;
            }
                                    
            ++I2;
        }

        ++I1;
    }
}

In my next post, I’ll likely discuss integrating this navigation mesh into the game simulation to test its feel, or I may explore subtracting static collisions from the mesh using my rewritten version of the Clipper2 library.

Thanks for reading, and I hope you found this post interesting and educational!

Step 1: Creating Native Polygons#

Step 2: Partitioning into Convex Polygons#

Step 3: Building Navigation Nodes for A* Pathfinding#

Step 4: Ensuring Consistent Vertex Ordering#

Step 5: Pathfinding with A* and the Funnel Algorithm#

Finding the Start and End Polygons#

Running A* Pathfinding#

Building the Portal Array#

Applying the Funnel Algorithm#

Conclusion#